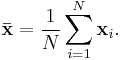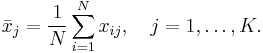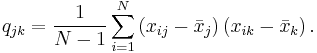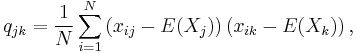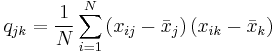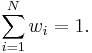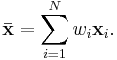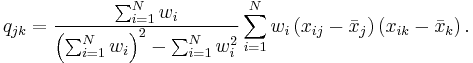Sample mean and sample covariance

The sample mean or empirical mean and the sample covariance are statistics computed from a collection of data on one or more random variables. The sample mean is a vector each of whose elements is the sample mean of one of the random variables – that is, each of whose elements is the average of the observed values of one of the variables. The sample covariance is a square matrix whose i, j element is the covariance between the sets of observed values of two of the variables and whose i, i element is the variance of the observed values of one of the variables. If only one variable has had values observed, then the sample mean is a single number (the average of the observed values of that variable) and the covariance matrix is also simply a single value (the variance of the observed values of that variable).

1 Sample mean and covariance
2 Variance of the sample mean
3 Weighted samples
4 Criticism
5 See also
6 References

Sample mean and covariance

Let 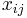$x_{ij}$ be the i^th independently drawn observation (i=1,...,N) on the j^th random variable (j=1,...,K), and arrange them in an N × K matrix, with row i denoted 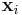$\mathbf{x}_i$ (i=1,...,N).

The sample mean vector 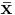$\mathbf{\bar{x}}$ is a row vector whose j^th element (j = 1, ..., K) is the average value of the N observations on the j^th random variable. Thus the sample mean vector is the average of the row vectors of observations on the K variables:

$\mathbf{\bar{x}}=\frac{1}{N}\sum_{i=1}^{N}\mathbf{x}_i.$

Here the individual element j of the sample mean vector, the mean of the j^th random variable, is

$\bar{x}_{j}=\frac{1}{N}\sum_{i=1}^{N}x_{ij},\quad j=1,\ldots,K.$

The sample covariance of N observations on the K variables is the K-by-K matrix $\textstyle \mathbf{Q}=\left[ q_{jk}\right]$ with the entries given by

$q_{jk}=\frac{1}{N-1}\sum_{i=1}^{N}\left( x_{ij}-\bar{x}_j \right) \left( x_{ik}-\bar{x}_k \right) .$

The sample mean and the sample covariance matrix are unbiased estimates of the mean and the covariance matrix of the random vector 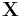$\textstyle \mathbf{X}$ , a row vector whose j^th element (j = 1, ..., K) is one of the random variables. The sample covariance matrix has 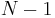$\textstyle N-1$ in the denominator rather than 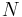$\textstyle N$ due to a variant of Bessel's correction: In short, the sample covariance relies on the difference between each observation and the sample mean, but the sample mean is slightly correlated with each observation since it's defined in terms of all observations. If the population mean 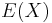$E(X)$ is known, the analogous unbiased estimate

$q_{jk}=\frac{1}{N}\sum_{i=1}^N \left( x_{ij}-E(X_j)\right) \left( x_{ik}-E(X_k)\right),$

using the population mean, has 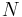$\textstyle N$ in the denominator. This is an example of why in probability and statistics it is essential to distinguish between upper case letters (random variables) and lower case letters (realizations of the random variables).

The maximum likelihood estimate of the covariance

$q_{jk}=\frac{1}{N}\sum_{i=1}^N \left( x_{ij}-\bar{x}_j \right) \left( x_{ik}-\bar{x}_k \right)$

for the Gaussian distribution case has N in the denominator as well. The ratio of 1/N to 1/(N − 1) approaches 1 for large N, so the maximum likelihood estimate approximately equals the unbiased estimate when the sample is large.

Variance of the sample mean

For each random variable, the sample mean makes a good estimator of the population mean, as its expected value is the same as the random variable's population mean, but it is not exact: different samples drawn from the same distribution will give different sample means and hence different estimates of the mean of the random variable's population. Thus the sample mean is a random variable, not a constant, and consequently it will have its own distribution. 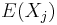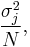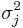For a random sample of N observations on the j^th random variable, the sample mean's distribution itself has mean equal to the population mean $E(X_j)$ and variance equal to $\frac{\sigma^2_j}{N},$ where $\sigma^2_j$ is the variance of the random variable X_j.

Weighted samples

In a weighted sample, each vector 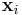$\textstyle \textbf{x}_{i}$ (each set of single observations on each of the K random variables) is assigned a weight 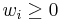$\textstyle w_i \geq0$ . Without loss of generality, assume that the weights are normalized:

$\sum_{i=1}^{N}w_i = 1.$

(If they are not, divide the weights by their sum.) Then the weighted mean vector 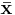$\textstyle \mathbf{\bar{x}}$ and the weighted covariance matrix $\textstyle \mathbf{Q}=\left[ q_{jk}\right]$ are given by

$\mathbf{\bar{x}}=\sum_{i=1}^N w_i \mathbf{x}_i.$

Therefore, in the most general case^[1]

$q_{jk}=\frac{\sum_{i=1}^{N}w_i}{\left(\sum_{i=1}^{N}w_i\right)^2-\sum_{i=1}^{N}w_i^2} \sum_{i=1}^N w_i \left( x_{ij}-\bar{x}_j \right) \left( x_{ik}-\bar{x}_k \right) .$

If all weights are the same, 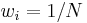$\textstyle w_{i}=1/N$ , the weighted mean and covariance reduce to the sample mean and covariance above.

Criticism

The sample mean and sample covariance are widely used in statistics and applications, and are extremely common measures of location and dispersion, respectively, likely the most common: they are easily calculated and possess desirable characteristics.

However, they suffer from certain drawbacks; notably, they are not robust statistics, meaning that they are sensitive to outliers. As robustness is often a desired trait, particularly in real-world applications, robust alternatives may prove desirable, notably quantile-based statistics such the sample median for location,^[2] and interquartile range (IQR) for dispersion. Other alternatives include trimming and Winsorising, as in the trimmed mean and the Winsorized mean.

References

^ Mark Galassi, Jim Davies, James Theiler, Brian Gough, Gerard Jungman, Michael Booth, and Fabrice Rossi. GNU Scientific Library - Reference manual, Version 1.15, 2011. Sec. 21.7 Weighted Samples
^ The World Question Center 2006: The Sample Mean, Bart Kosko